Large Language Models (LLMs) don't just generate text. They generate a sequence of tokens, and every token comes with a log probability (logprob). These logprobs can be used to estimate how confident the model was in its output.
For example, when we ask a language model “what is the capital of France?” the model generates a sequence of tokens and logprobs.

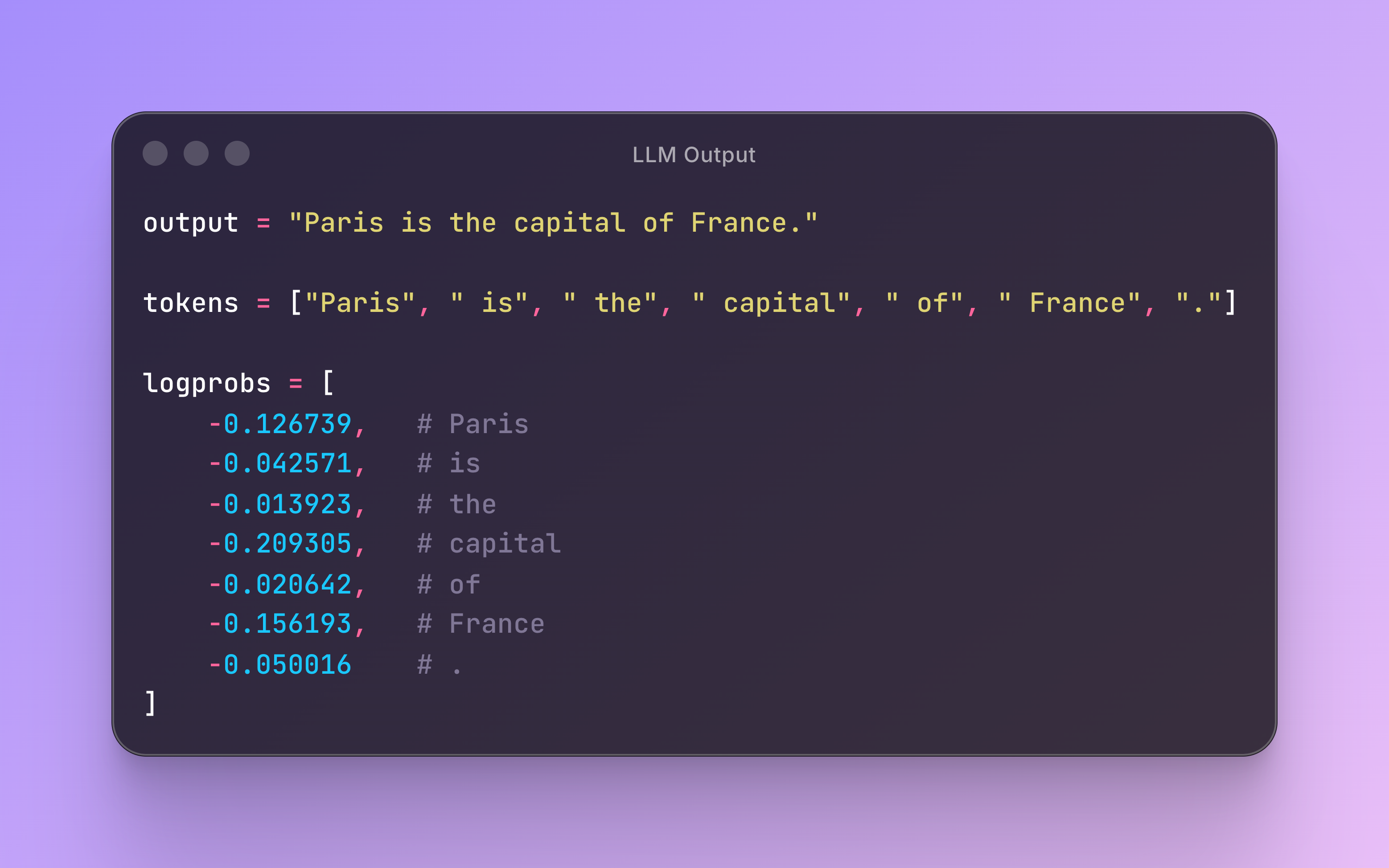
We can then use these logprobs to calculate a confidence score for the model output. A common approach is to calculate the geometric mean of token probabilities, which is mathematically equivalent to exponentiating the mean of logprobs:
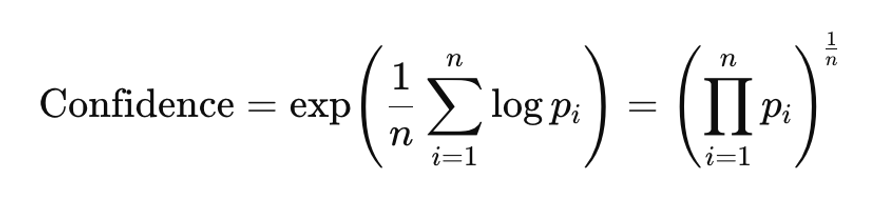

Structured Output Confidence
Structured outputs make LLMs far more usable for enterprise applications, especially text analytics that involve classification, extraction, abstraction, etc.
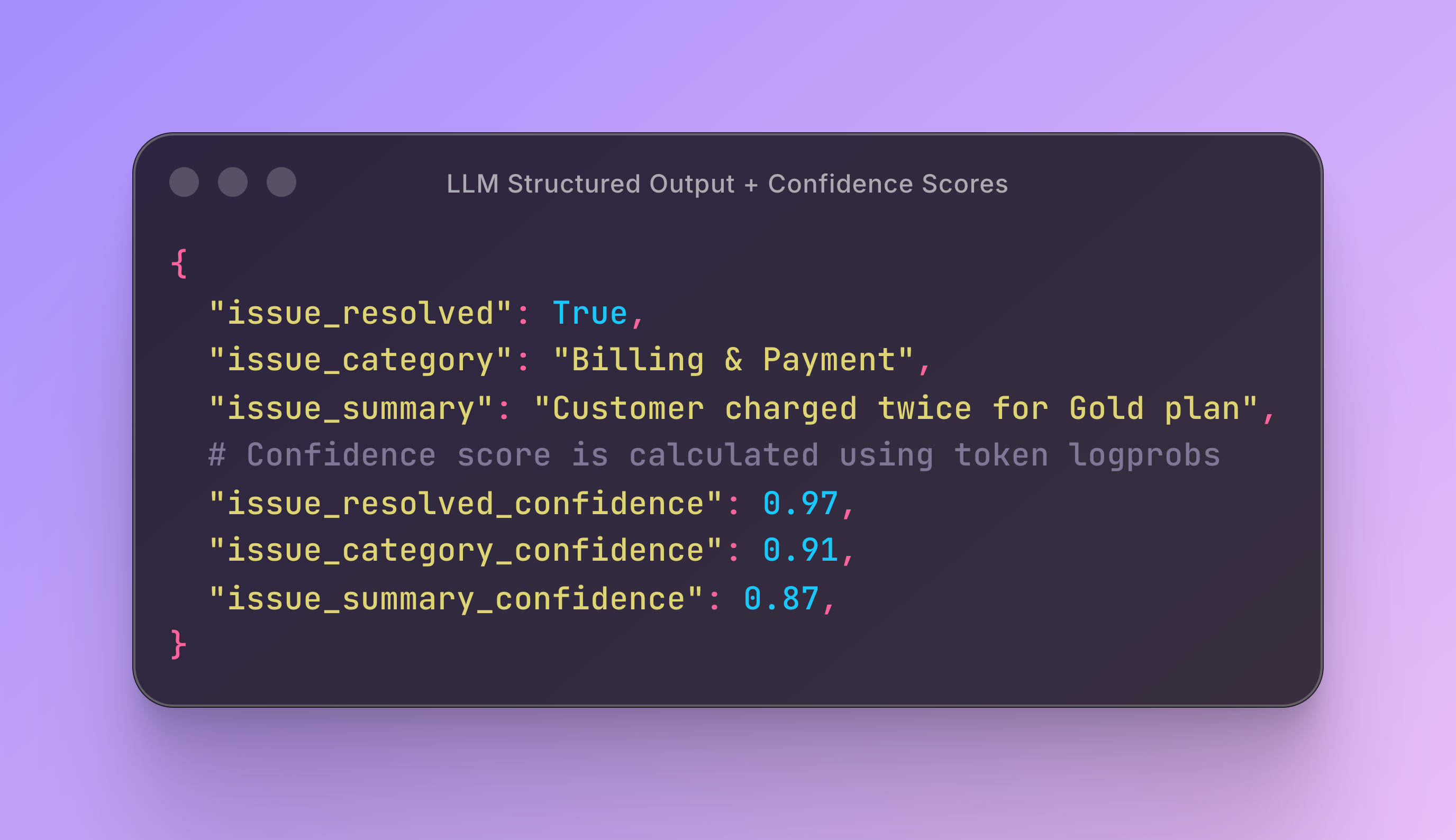
If you're working with structured outputs like JSON, you can take it a step further and estimate field-level confidence. Instead of one confidence score for the entire output, you get a separate confidence score for each field. This is crucial because not all parts of a JSON response are equally important, and we need granular confidence scores to know which fields to trust.
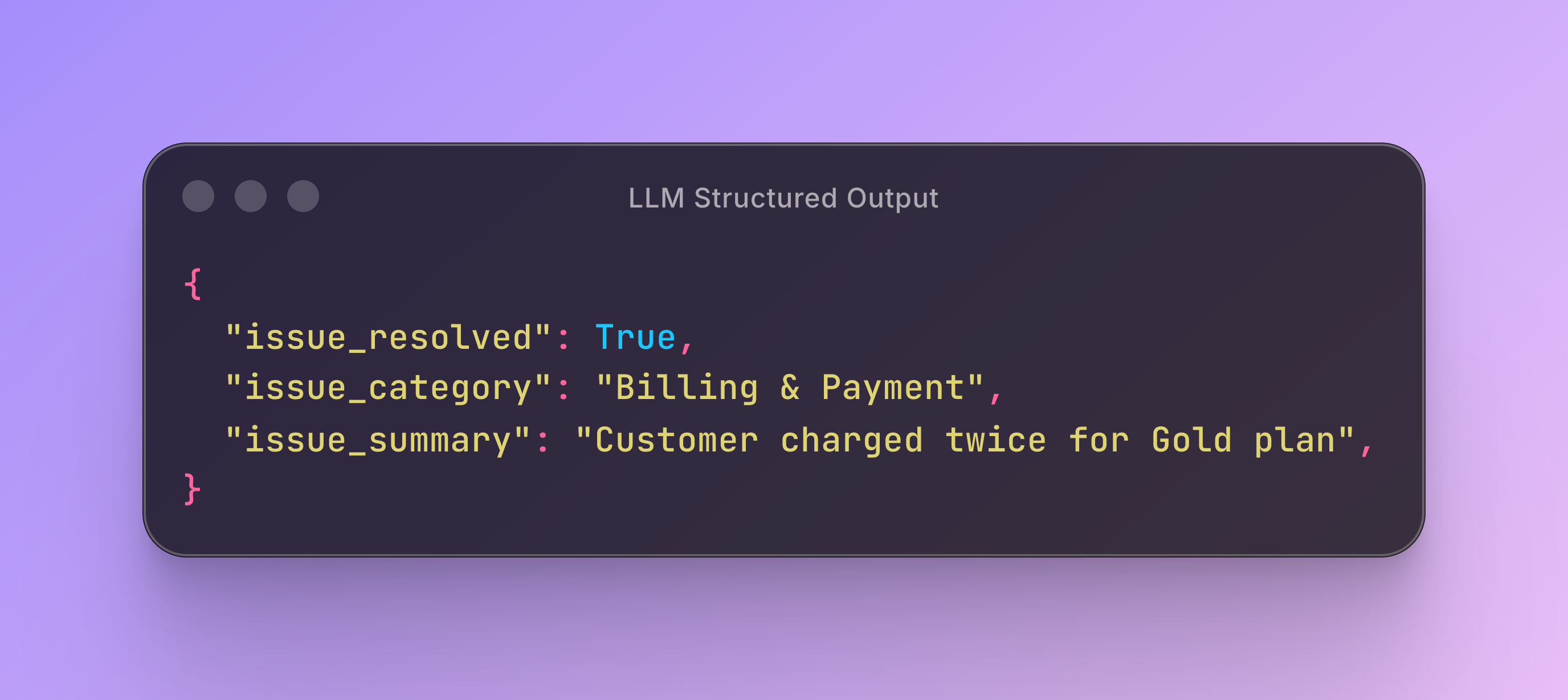
For example, what if we require the LLM to generate JSON that conforms to a schema with an “answer” field? Here, the LLM generates a key-value pair.


We can see that the JSON output contains tokens that matter (tokens for “Paris is the capital of France.”) and tokens that don't matter (punctuation, braces, quotes, schema field names). We can't simply compute confidence by averaging over all tokens in the output. The model can be extremely confident in the JSON format, even when it's wrong about the answer. This is because punctuation, braces, quotes, and schema field names are highly predictable, even when the actual value is incorrect.
For enterprise use cases such as classification and summarization, what matters is field-level confidence, not “how confident the model is that it knows how to type a JSON brace.”
By extracting field-level confidence, we can augment the structured output with confidence scores for each field:

This requires aligning each key-value field with its corresponding token span in the raw output. And that alignment problem is trickier than it looks.
The Token Alignment Problem
LLMs produce a flat sequence of tokens but JSON is hierarchical and can be deeply nested.
To calculate field-level confidence for a JSON output, we need to:
- Parse the JSON
- Identify the exact substring corresponding to the key-value pair
- Align that substring with the correct token span in the generated output
- Aggregate those token-level logprobs into a field-level confidence score
- Do this efficiently, even for large or deeply nested JSON
At Queryboost, we've developed a linear time algorithm for computing structured output confidence for arbitrary JSON generated by LLMs (including deeply nested JSON). Our custom algorithm is based on the Aho-Corasick algorithm and runs in O(L + K) time where L is the length of the output and K is the number of fields.
This is what enables our AI data processor to quickly generate structured output with field-level confidence scores.
Benchmark: Does Structured Confidence Actually Help?
To evaluate the real utility of field-level confidence, let's run a simple experiment on the BoolQ dataset (validation split) using the Qwen3 1.7B model. BoolQ is a binary-classification reading-comprehension task where the model answers a yes/no question based on a passage.
We prompt the model to predict True/False and generate output that conforms to this JSON schema:

Experimental Setup
We compare two approaches to confidence scoring. For both methods, we need to convert confidence scores to P(True) — the probability that the answer is True. This standardization is required for AUC-ROC calculation, which measures how well the P(True) scores separate ground-truth True labels from False labels.
Method 1: Field-Level Confidence
- • Extract only the token logprobs for the value (True or False)
- • Get confidence score using only the logprob for the True or False token
- • If the model predicted True, use the confidence score for P(True). If the model predicted False, use 1 - confidence score for P(True)
Method 2: Sequence-Level Confidence (Baseline)
- • Get logprobs for all tokens in the output
- • Get confidence score using all token logprobs
- • Calculate P(True) the same way as Method 1
Both methods produce a P(True) score for each prediction, which we then evaluate using AUC-ROC against the ground truth BoolQ labels.
Results
Field-Level Confidence
0.7609
AUC-ROC
Sequence-Level Confidence
0.7428
AUC-ROC
Why Does Field-Level Confidence Win?
Sequence-level confidence gets inflated by highly predictable structural tokens:
- JSON syntax:
{,},",: - Schema field names like “answer”
- Punctuation and formatting
The model is extremely confident about these tokens, even when the actual answer is wrong. This creates misleading confidence scores.
Field-level confidence solves this by focusing exclusively on the tokens that represent the actual answer, producing a more accurate and reliable estimate of model certainty.
We can see this difference clearly in the distribution of P(True) for each method. P(True) based on sequence-level confidence is heavily concentrated at the extremes (very low or very high), while P(True) based on field-level confidence spreads across a much broader range:
Distribution of P(True) by Confidence Method
| P(True) Buckets | Field-Level | Sequence-Level |
|---|---|---|
| 0.0 - 0.1 | 1,790 | 1,901 |
| 0.1 - 0.2 | 59 | 0 |
| 0.2 - 0.3 | 52 | 0 |
| 0.3 - 0.4 | 0 | 0 |
| 0.4 - 0.5 | 0 | 0 |
| 0.5 - 0.6 | 0 | 0 |
| 0.6 - 0.7 | 0 | 0 |
| 0.7 - 0.8 | 58 | 0 |
| 0.8 - 0.9 | 61 | 26 |
| 0.9 - 1.0 | 1,250 | 1,343 |
| Total | 3,270 | 3,270 |
Field-level confidence produces a better-calibrated distribution of P(True) values, enabling more reliable and actionable decisions in real-world settings.
Looking Ahead
This experiment used a very simple schema: a single boolean field.
But the same idea extends naturally to:
- Complex schemas with dozens of fields
- Nested objects and hierarchical structures
- Lists and arrays
- Real-world extraction and classification tasks
For example, here's a more complex structured output with multiple fields:
With field-level confidence scoring, each field gets its own confidence score:
Conclusion
Field-level confidence transforms how we evaluate and trust LLM outputs. By focusing on what matters, we get better calibration, more accurate reliability estimates, and ultimately more useful systems.
As LLMs become more capable and structured outputs become the norm for enterprise applications, confidence scoring will shift from a nice-to-have to a requirement. The question isn't whether to use confidence scores, but how granular and accurate those scores need to be.
At Queryboost, we're building the infrastructure to make field-level confidence scoring fast, accurate, and accessible at scale.
Johnson Kuan
Founder & CEO, Queryboost